前回の続きです。回生はしない方がいいのか、を3つに分けて考えます。
前回は1つ目について考えましたが、今回は2つ目ではなく、いきなり
3つ目に飛びます。下り坂で回生した方がいいのか、です。

さて、こんな下り坂があったらどうするとよいでしょうか、ということを
今回考えます。
1)回生しながら下る
2)惰性走行(ゼロアンペア)して、ポテンシャルエネルギーを速度に変換する、つまり加速する
どちらがよいのでしょうか。
要するに、ポテンシャルエネルギーをバッテリーに入れた方がいいのか、速度に換えた方がいいのか、です。
先に結論を書いちゃいます。
結論は、低速かつ短くて緩い坂なら回生しない方がいい場合もあるが、基本的には
速度を増やさずに回生した方がいい、です。
さて、先ほどの下り坂を図にするとこんな感じですね。初速は仮に60km/hとしましょう。
それで、速度に換えるのと回生とを図に表すと・・・
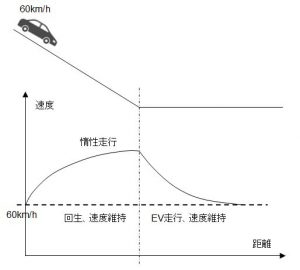
こんな感じになります。ブレーキを踏む方は60km/hを維持するようにブレーキを
踏んで(充電して)、平地になったら、60km/hを維持するようなEV走行(放電)をします。
一方、惰性走行は平地になるまで加速して、そのまま惰性のまま、平地につっこむので
速度はいつか60km/hに戻ります。
勝負は、その地点で回生側のSOCが上がっていれば回生の勝ち、下がっていれば惰性の勝ちです。
それで、惰性の速度が加速時に上にふくらんだ形(速度が上がるほど加速しにくい)、減速時に
下にふくらんだ形になる理由ですが・・・
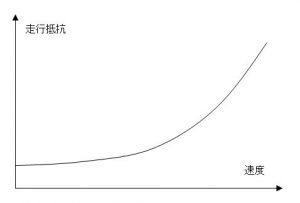
走行抵抗の形がこんな具合に速度が上がるほど増加するからです。
速度が上がるほど抵抗が増すので速度が上がりにくくなるということです。
ちなみに、速度に対して走行抵抗が一定なら(速度が変わっても走行抵抗が変わらないなら)
こんな感じになります。
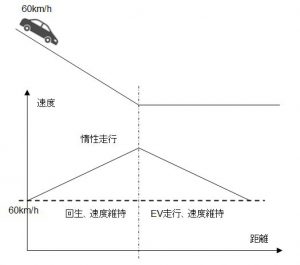
ちょっとウソっぽいですが・・・言いたいことは、速度の上がり方、下がり方つまり加減速が一定になるということです。
ウソっぽいというのは、坂の勾配によって、上がり方と下がり方は違うので、加減速の角度は違うということです。
(図では同じように書いていますが)
で、この簡単なやつでまずは考えてみます。
下り坂ではポテンシャルエネルギーが速度に変換されますが、その量は、車を押す力×距離となります。
車を押す力は下り坂の重力mgsinθ-走行抵抗(一定)=Fslopeとしましょう。
例えば100秒下るとして、距離は、(60+Fslope/m×50)×100となります。
平地では、速度が走行抵抗で消費されますが、その量は車を押す力×距離となります。
車を押す力は走行抵抗なので、mgsinθ-Fslopeとなります。
先ほど増えた速度はFslope/m×100ですが、それを戻す時間はFslope/m×100/((mgsinθ-Fslope)/m)
ですので、Fslope/(mgsinθ-Fslope)×100です。
下りの「距離は」と書いたところの速度部分「(60+Fslope/m×50)」は平地も同じで、
秒数がどうか、なのですが、秒数は押す力の比であるので、仕事量は同じということになります。
ということは、回生して得られるであろうエネルギーと放電するエネルギーが同じになるので、
(例えば、60km/hから平地までに100kJを得たとして、平地で60km/hになるまで
惰性走行した時に消費した走行抵抗の積算が100kJだったということ)
回生の効率が1以下であることを考慮すると、例えば100kJが80kJに減って、平地で100kJの
走行抵抗を生み出すバッテリーエネルギーは100kJではもちろん済まず、120kJとか増加することを
考慮すると、回生せずに速度に変換した方がいいことになります。
続きは次回です。
